Tuesday 28 February 2017
The Moon is a Mirror
Toward the end of his life, King Raeldus built an enormous palace of spiritual marvels. Fearful of punishment in the afterlife, he hoped to win favor with the unseen world.
To this end, he stocked his palace with altars to every cult and religion he could find. Through donations, command, and threats, he saw that every one of them was maintained by representatives of the religion. In some cases, whole splinter sects were transplanted to the palace.
Foolish of that sort never lasts long, and a century later the palace was home only to ghosts, animals and the occasional bandit. That is, until the Sage of Lune arrived.
A fittingly remote place to carry out her work, for years the Sage used her mystical lenses to scry out omens and prophecies by gazing at the surface of the moon. She called it a mirror, a reflection of our earthly existence, and said that the mirror image of every person.
Those willing to make the long trek to the palace, and the harrowing trek through the palace itself, could be sure of a wise insight as a reward for their efforts.
Wednesday 22 February 2017
Isometric Dungeon #5 - Cavern Waterfall
Here's a fifth video in my isometric dungeon drawing series, a cavern waterfall.
This time it's a cavern waterfall. I don't say much, although I had fun with the audio regardless. Happy to take requests - what has stumped or intimidated you in the past?
Monday 20 February 2017
Trilemma Adventures Known World Map
As those of you following along may have discerned, there's a nominal campaign setting where I situate my adventures.
I will eventually detail the cultures and history of the place, although even once I've done that, I expect that most people will take the adventures and either use them as one-shots, or reskin them and put them into their own campaign setting.
To that end I'll provide a glossary of terms that will need adapting or hooking into your own campaign setting. The Seree are a magocratic precursor civilization; the Martoi a bunch of half-undead fey, and so on.
Tuesday 14 February 2017
Curves in Isometric Mapping
A recent post in a G+ map-making community highlighted how difficult it is to draw curved objects in isometric maps.
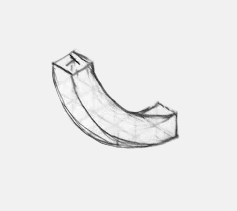
Here's a typical, challenging object: a curved chute that drops from a trap door into a lower level.
This is a worthy attempt at a complicated shape, but as you can see it doesn't look quite right; it looks a bit twisted, like licorice.
The main problems seem to be two-fold:
1. How the $#*@! do you draw a nice curve?
2. How do you take that curved surface and extude it into a three-dimensional shape?
Here's a typical, challenging object: a curved chute that drops from a trap door into a lower level.
This is a worthy attempt at a complicated shape, but as you can see it doesn't look quite right; it looks a bit twisted, like licorice.
The main problems seem to be two-fold:
1. How the $#*@! do you draw a nice curve?
2. How do you take that curved surface and extude it into a three-dimensional shape?
Drawing Isometric Circles
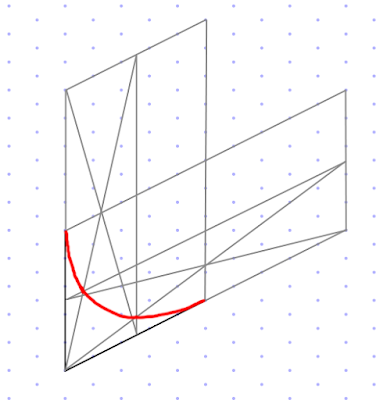
I've taken a stab at this before, but I've found a couple of ways that are a lot easier. Here's the basic structure, taken from this excellent blog post by Douglas Flynt:
That blog post spends a lot of time on subdividing the original square, but on isometric graph paper it's a lot easier. I'm drawing the outer curve of the chute, which has a radius of five squares:
Next step is to draw the inner curve, which has a radius of four squares:
Erasing my construction lines, I'm left with this shape:
Extruding the Shape
Now I need to extrude this into a three-dimensional form. The trick to doing this is to draw exactly the same curves one square over:
With a bit of practice you can manage this freehand, until then, you may need to set up the curve-drawing framework you used for the original lines.
Once you've got this, follow the northwest-southeast axis to "tie" the two sets of curves together. In the lower left, you're drawing a tangent across the two sets of curves:
Then, trace the lines that will be visible to get the outline of the final form:
It's still a little bit wonky; as always I recommend doing all your construction work in pencil (or better yet, with blue pencil/marker so you can pull it out with Photoshop), so you have lots of tries at the freehand curves.
Subscribe to:
Posts (Atom)